FOREST FIRES IN BRAZIL

See https://www.kaggle.com/gustavomodelli/forest-fires-in-brazil for a full description of the dataset.

Import packages

import pandas as pd #Handle datasets
import seaborn as sns #Plots
import matplotlib.pyplot as plt  #Plots
import matplotlib

#Set some graphical parameters
rc={'axes.labelsize': 25, 'figure.figsize': (20,10), 
    'axes.titlesize': 25, 'xtick.labelsize': 18, 'ytick.labelsize': 18}
sns.set(rc=rc)

#Path data
path = 'C:/Users/Andreella/Desktop/Doc/GitHub/angeella.github.io/Data'
df = pd.read_csv(path + '/amazon.csv',encoding="ISO-8859-1")

First \(3\) observations:

df.head(n=3)

##    year state    month  number        date
## 0  1998  Acre  Janeiro     0.0  1998-01-01
## 1  1999  Acre  Janeiro     0.0  1999-01-01
## 2  2000  Acre  Janeiro     0.0  2000-01-01

Some information about the variables:

df.info()

## <class 'pandas.core.frame.DataFrame'>
## RangeIndex: 6454 entries, 0 to 6453
## Data columns (total 5 columns):
##  #   Column  Non-Null Count  Dtype  
## ---  ------  --------------  -----  
##  0   year    6454 non-null   int64  
##  1   state   6454 non-null   object 
##  2   month   6454 non-null   object 
##  3   number  6454 non-null   float64
##  4   date    6454 non-null   object 
## dtypes: float64(1), int64(1), object(3)
## memory usage: 252.2+ KB

We are interested about the number of forest fires in Brazil

df.number.describe()

## count    6454.000000
## mean      108.293163
## std       190.812242
## min         0.000000
## 25%         3.000000
## 50%        24.000000
## 75%       113.000000
## max       998.000000
## Name: number, dtype: float64

To have an simple plot, we take a subset of the dataset:

df1 = df[(df.year > 2010) & (df.year < 2019)]
df1 =df1.loc[(df1.state.str.startswith('M'))]

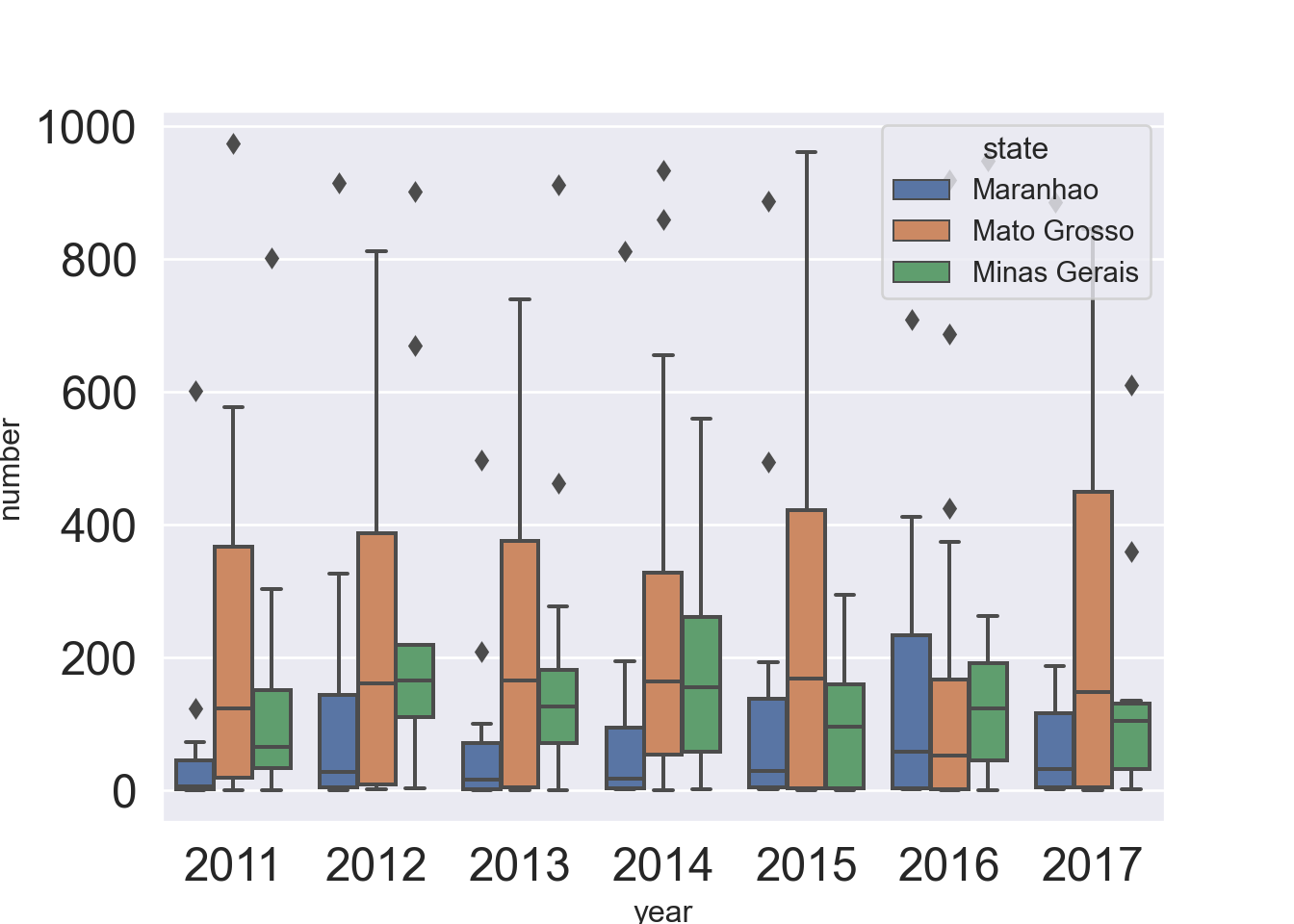
We do a boxplot about the number of fire by groups, i.e., the states and the years.

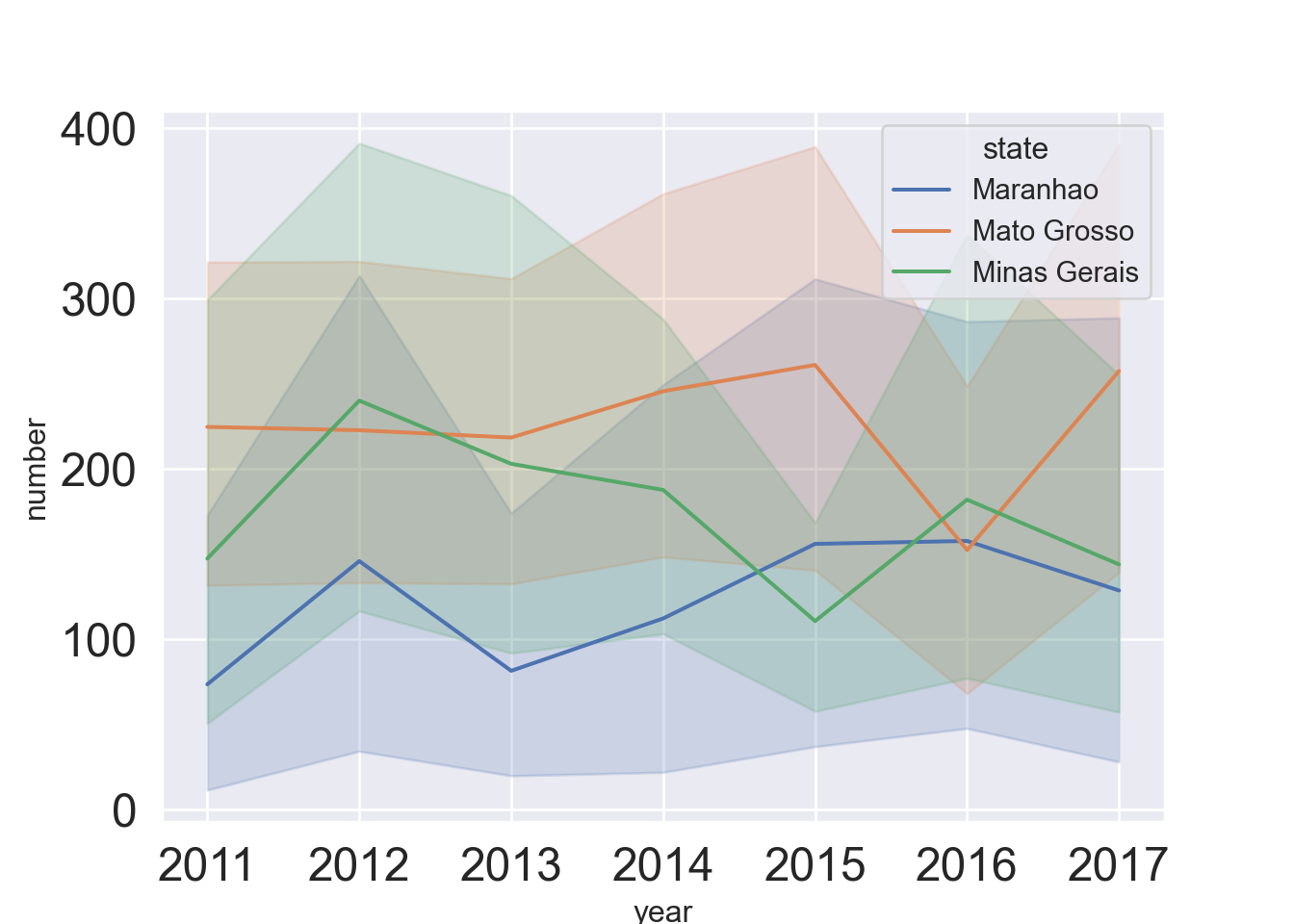
sns.boxplot(x = 'year', y = 'number', hue = "state", data = df1)

We do a timeseries plot with error bands:

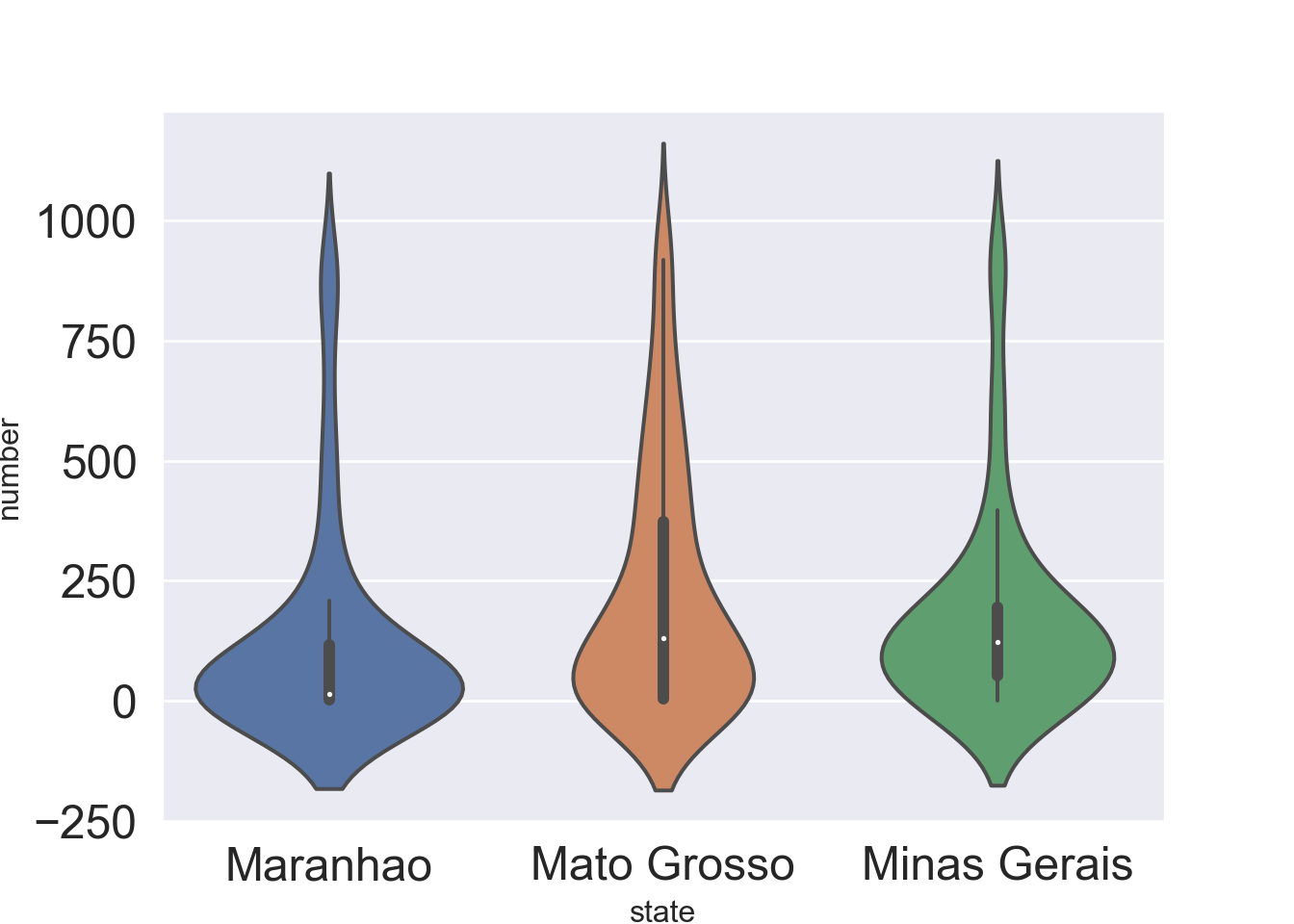
sns.lineplot(x="year", y="number",hue="state", data=df1)

also we do a grouped violinplots:

sns.violinplot(x="state", y="number", data=df1)

For other plots, please refers to https://seaborn.pydata.org/examples/index.html.

ECONOMIC FREEDOM INDEX

See https://www.kaggle.com/lewisduncan93/the-economic-freedom-index for a full description of the dataset.

Load and preprocess data

dt = pd.read_csv(path + '/economic_freedom_index2019_data.csv',encoding="ISO-8859-1")
dt.columns = dt.columns.str.replace(' ', '')
dt.columns = dt.columns.str.replace('2019', '')
dt.columns = dt.columns.str.replace('%', '')
dt.columns = dt.columns.str.replace('(', '')

## <string>:1: FutureWarning: The default value of regex will change from True to False in a future version. In addition, single character regular expressions will *not* be treated as literal strings when regex=True.

dt.columns = dt.columns.str.replace(')', '')

## <string>:1: FutureWarning: The default value of regex will change from True to False in a future version. In addition, single character regular expressions will *not* be treated as literal strings when regex=True.

dt = dt.dropna(axis = 0,how='any')

Basic info

dt.info()

## <class 'pandas.core.frame.DataFrame'>
## Int64Index: 173 entries, 0 to 185
## Data columns (total 34 columns):
##  #   Column                 Non-Null Count  Dtype  
## ---  ------                 --------------  -----  
##  0   CountryID              173 non-null    int64  
##  1   CountryName            173 non-null    object 
##  2   WEBNAME                173 non-null    object 
##  3   Region                 173 non-null    object 
##  4   WorldRank              173 non-null    float64
##  5   RegionRank             173 non-null    float64
##  6   Score                  173 non-null    float64
##  7   PropertyRights         173 non-null    float64
##  8   JudicalEffectiveness   173 non-null    float64
##  9   GovernmentIntegrity    173 non-null    float64
##  10  TaxBurden              173 non-null    float64
##  11  Gov'tSpending          173 non-null    float64
##  12  FiscalHealth           173 non-null    float64
##  13  BusinessFreedom        173 non-null    float64
##  14  LaborFreedom           173 non-null    float64
##  15  MonetaryFreedom        173 non-null    float64
##  16  TradeFreedom           173 non-null    float64
##  17  InvestmentFreedom      173 non-null    float64
##  18  FinancialFreedom       173 non-null    float64
##  19  TariffRate             173 non-null    float64
##  20  IncomeTaxRate          173 non-null    float64
##  21  CorporateTaxRate       173 non-null    float64
##  22  TaxBurdenofGDP         173 non-null    float64
##  23  Gov'tExpenditureofGDP  173 non-null    float64
##  24  Country                173 non-null    object 
##  25  PopulationMillions     173 non-null    object 
##  26  GDPBillions,PPP        173 non-null    object 
##  27  GDPGrowthRate          173 non-null    float64
##  28  5YearGDPGrowthRate     173 non-null    float64
##  29  GDPperCapitaPPP        173 non-null    object 
##  30  Unemployment           173 non-null    object 
##  31  Inflation              173 non-null    float64
##  32  FDIInflowMillions      173 non-null    object 
##  33  PublicDebtofGDP        173 non-null    float64
## dtypes: float64(24), int64(1), object(9)
## memory usage: 47.3+ KB

Some plots

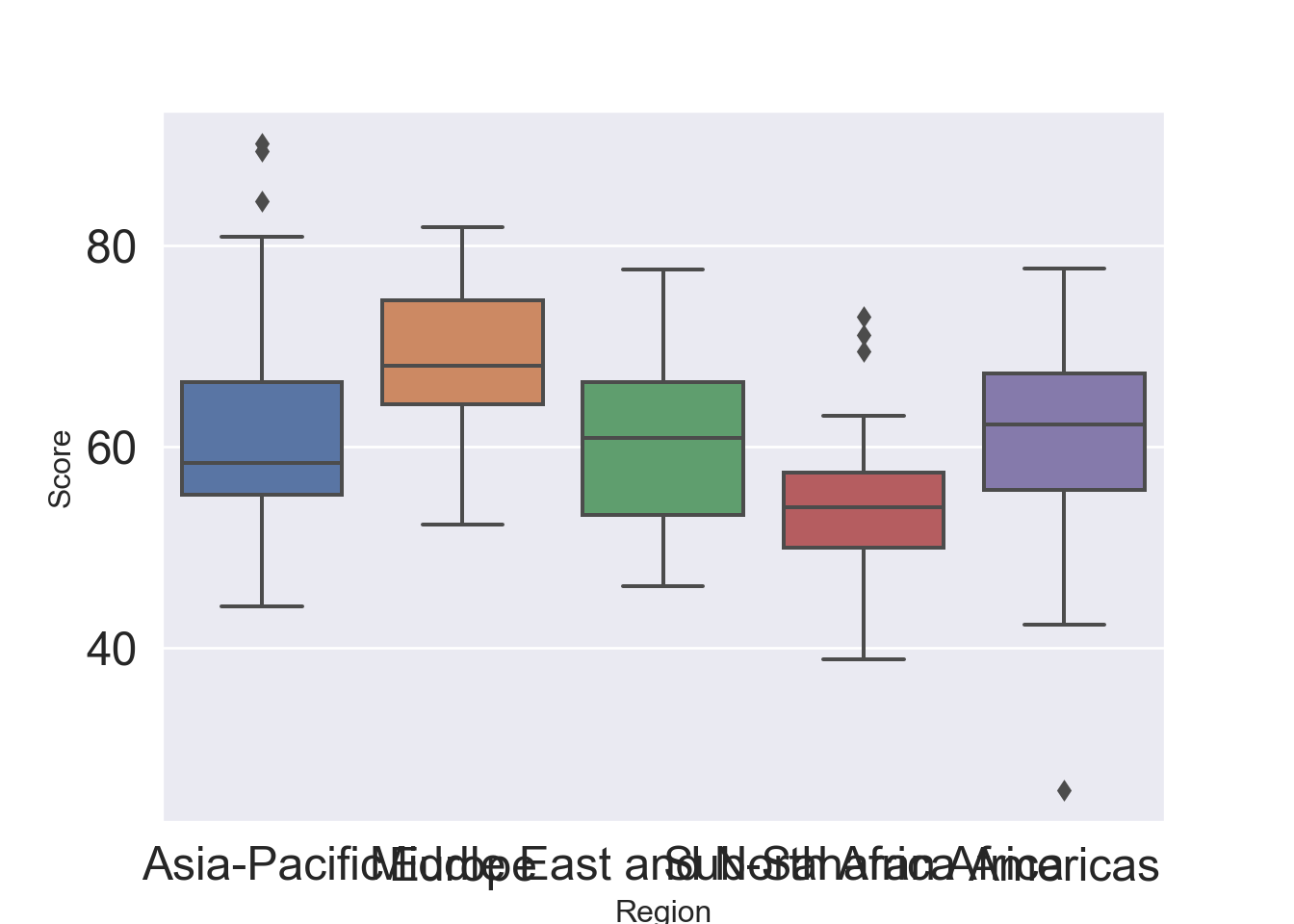
Boxplot by group, i.e. region:

sns.boxplot(x = 'Region', y = 'Score', data = dt)

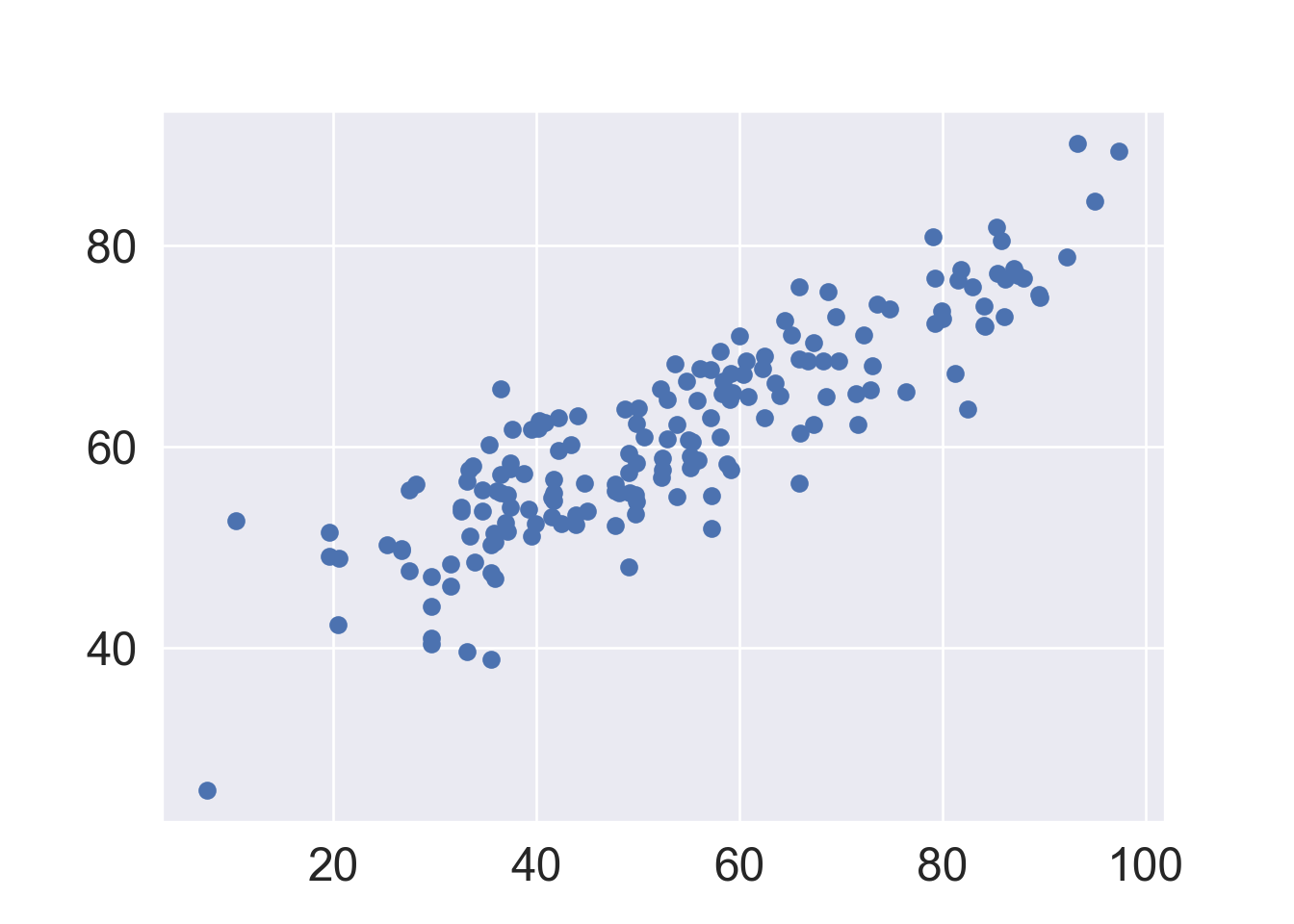
First scatter plot:

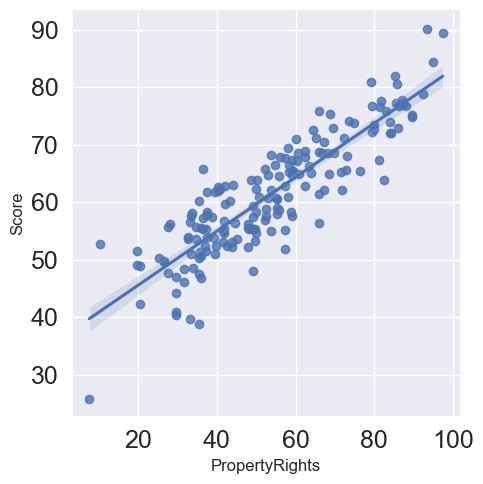
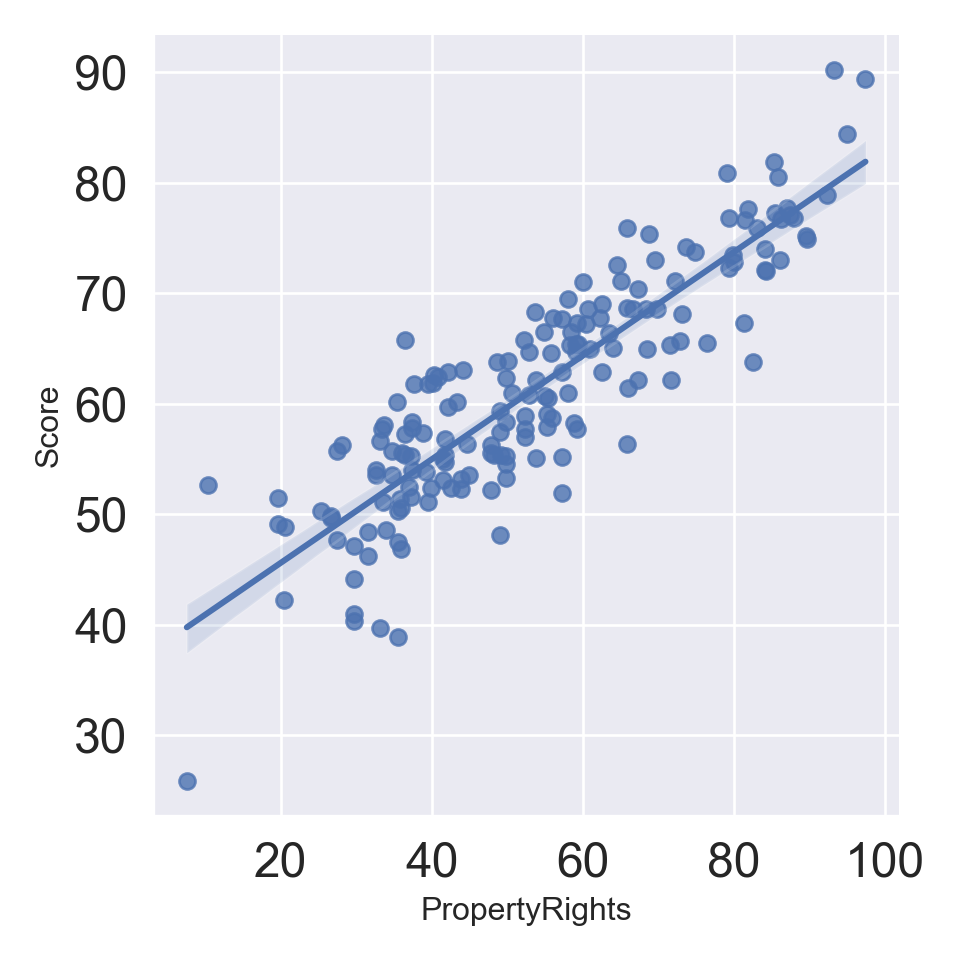
plt.scatter(x="PropertyRights", y="Score", data=dt)

We can put directly the linear regression fitting:

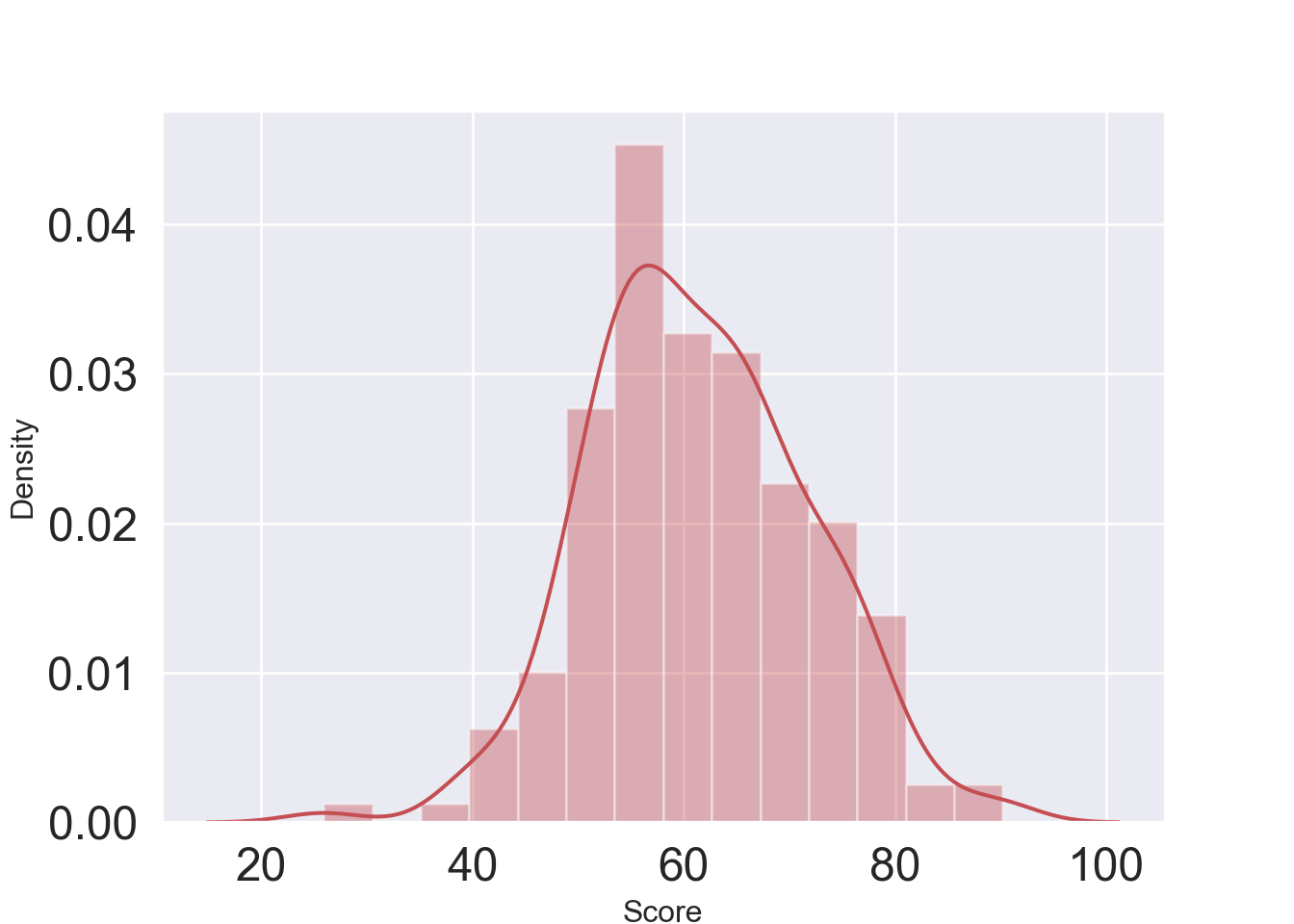
sns.lmplot(x="PropertyRights", y="Score", data=dt)

Density plot of the score variable:

sns.distplot(dt.Score, color="r")

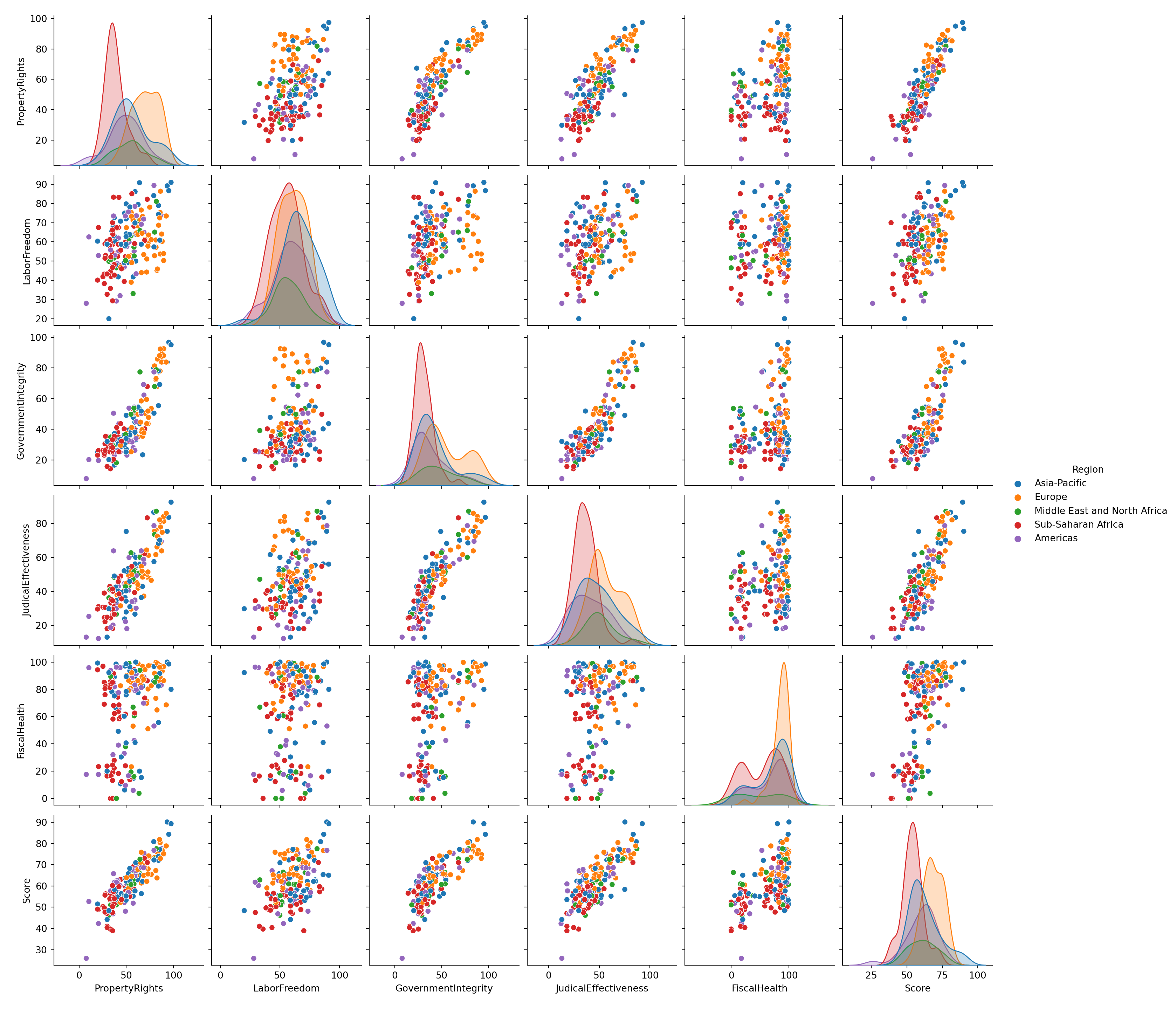
Pair plot considering some variables, i.e. Property Rights, Labor Freedom, Government Integrity, Judical Effectiveness, Fiscal Health, Region and Score:

dt1 = dt[['PropertyRights', 'LaborFreedom', 'GovernmentIntegrity', 'JudicalEffectiveness','FiscalHealth', "Score", 'Region']]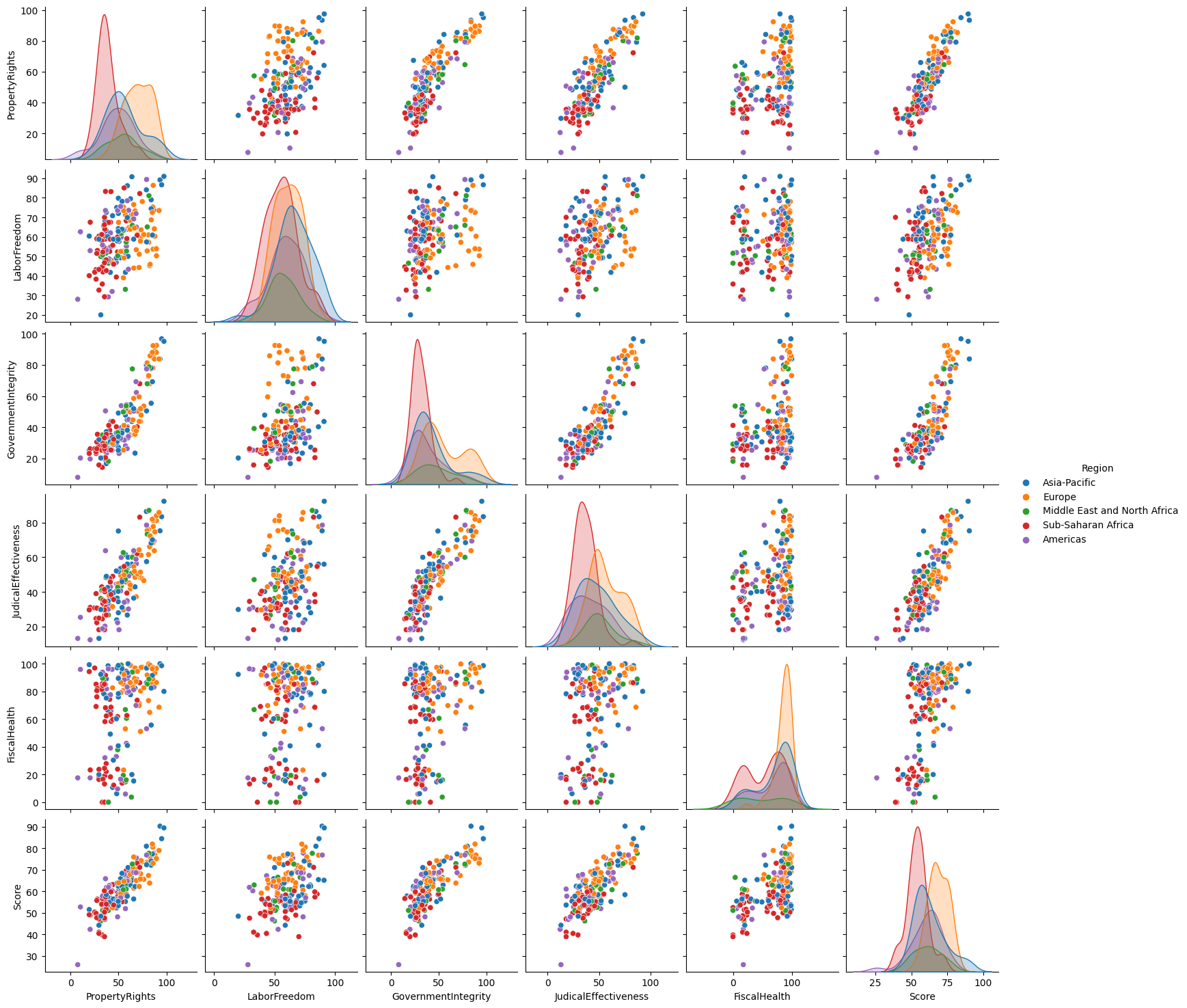

matplotlib.rc_file_defaults()
sns.pairplot(dt1, hue="Region")

Linear regression

Import packages

import statsmodels.api as sm
import statsmodels.formula.api as smf
from sklearn.metrics import mean_squared_error
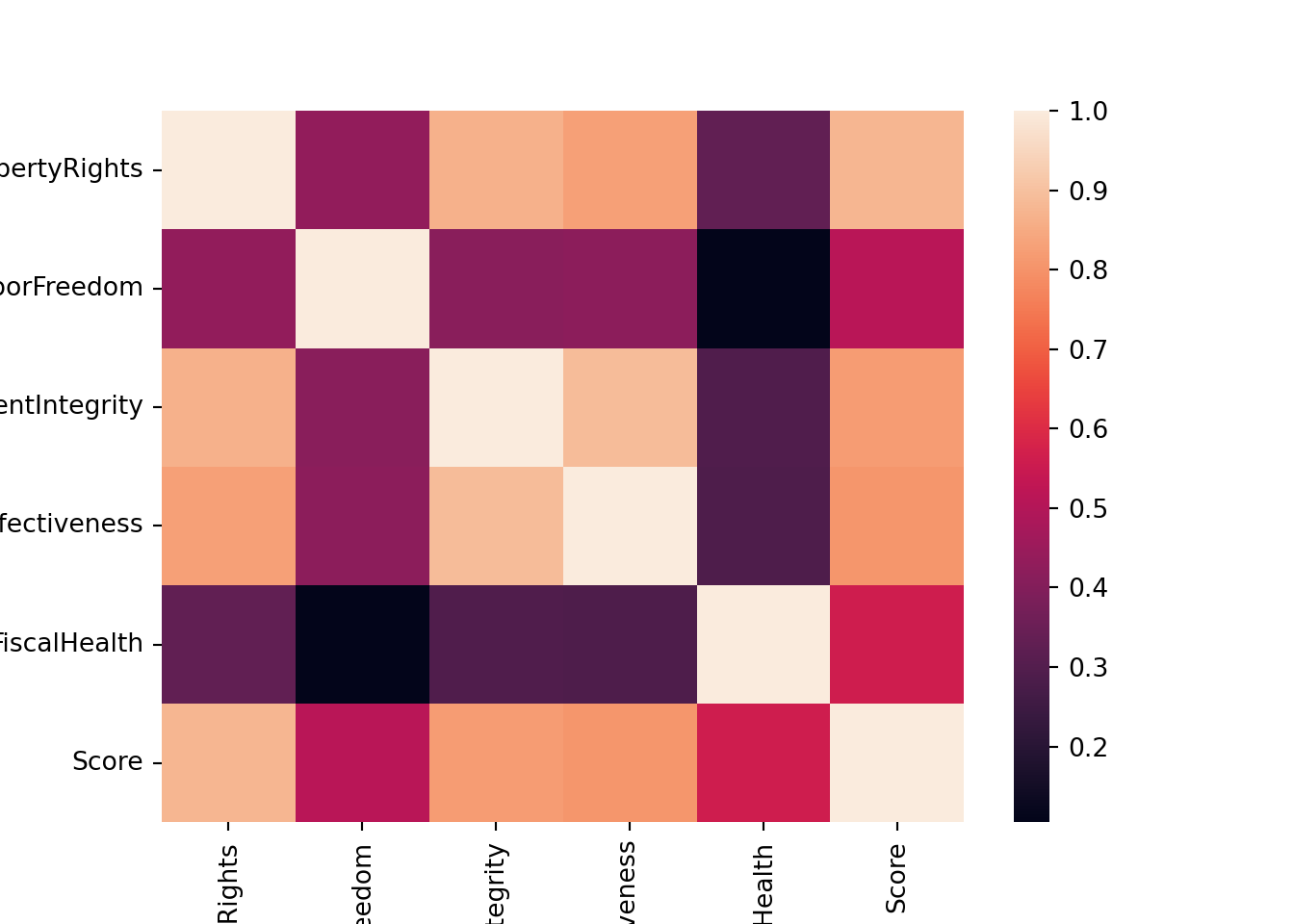
import sklearn

Correlation matrix

corr = dt[['PropertyRights', 'LaborFreedom', 'GovernmentIntegrity', 'JudicalEffectiveness','FiscalHealth', "Score"]].corr()
corr

##                       PropertyRights  LaborFreedom  ...  FiscalHealth     Score
## PropertyRights              1.000000      0.432746  ...      0.329969  0.876601
## LaborFreedom                0.432746      1.000000  ...      0.104431  0.512976
## GovernmentIntegrity         0.866998      0.413794  ...      0.292240  0.818174
## JudicalEffectiveness        0.826805      0.421694  ...      0.287380  0.805825
## FiscalHealth                0.329969      0.104431  ...      1.000000  0.559395
## Score                       0.876601      0.512976  ...      0.559395  1.000000
## 
## [6 rows x 6 columns]

Heatmap of the correlation matrix:

sns.heatmap(corr, 
        xticklabels=corr.columns,
        yticklabels=corr.columns)

We split the dataset into training (0.8) and test set (0.2):

import numpy as np
msk = np.random.rand(len(dt)) < 0.8
train = dt[msk]
test = dt[~msk]

Linear regression having as dependent variable the Score and PropertyRights, LaborFreedom and FiscalHealth as explicative variables:

results = smf.ols('Score ~ PropertyRights + LaborFreedom + FiscalHealth', data=train).fit()
results.summary()

OLS Regression Results
Dep. Variable:	Score	R-squared:	0.869
Model:	OLS	Adj. R-squared:	0.866
Method:	Least Squares	F-statistic:	282.3
Date:	Tue, 11 Nov 2025	Prob (F-statistic):	3.15e-56
Time:	11:13:31	Log-Likelihood:	-363.21
No. Observations:	132	AIC:	734.4
Df Residuals:	128	BIC:	745.9
Df Model:	3
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	27.3149	1.636	16.693	0.000	24.077	30.553
PropertyRights	0.3776	0.020	18.741	0.000	0.338	0.417
LaborFreedom	0.1158	0.028	4.207	0.000	0.061	0.170
FiscalHealth	0.1007	0.012	8.657	0.000	0.078	0.124

Omnibus:	4.401	Durbin-Watson:	1.700
Prob(Omnibus):	0.111	Jarque-Bera (JB):	4.266
Skew:	-0.440	Prob(JB):	0.118
Kurtosis:	2.969	Cond. No.	526.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

We predict the score values using the test set:

pred = results.predict(test)
plt.scatter(test.Score, pred,  color='b')

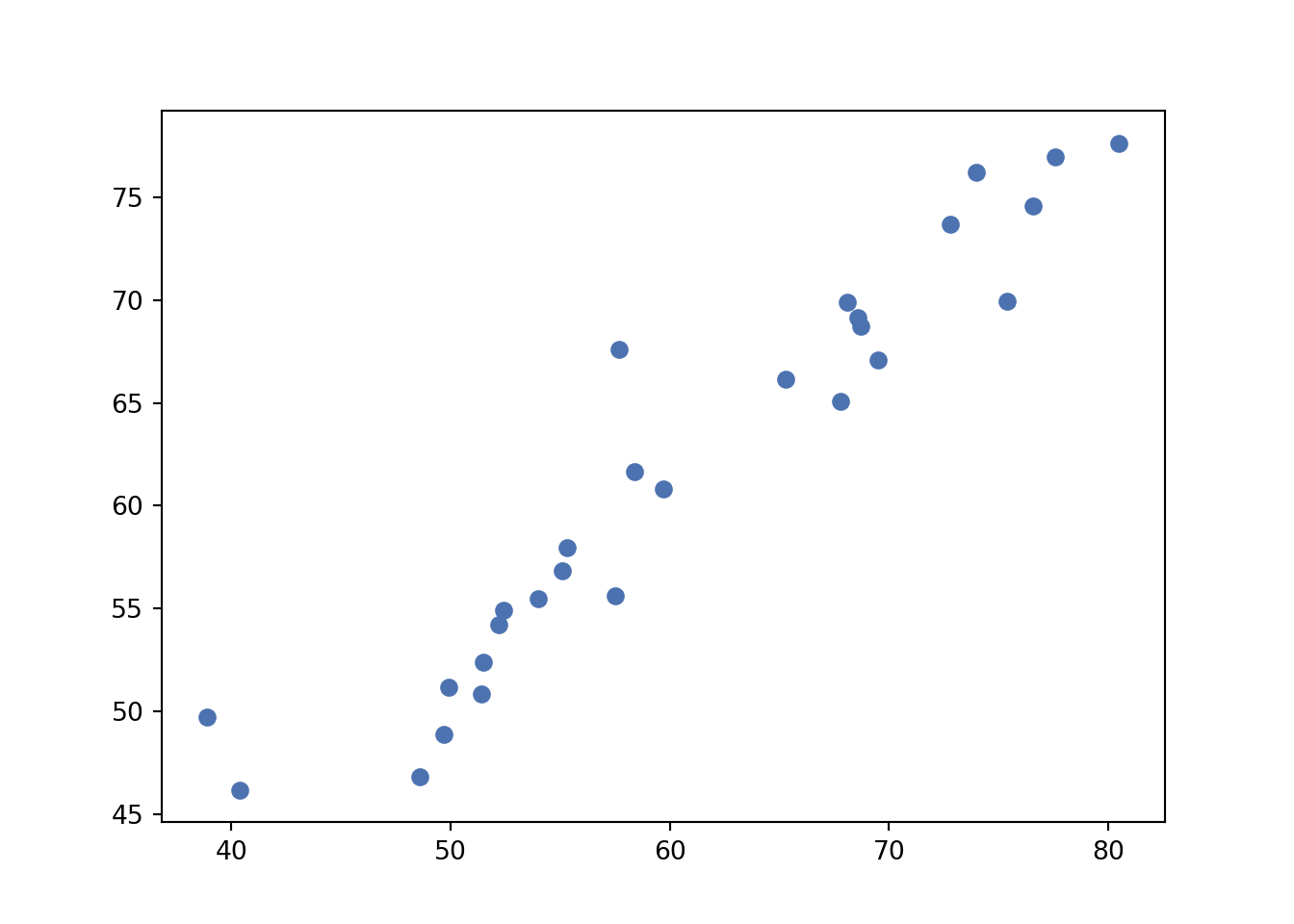
Compute the mean squared error:

mean_squared_error(test.Score, pred)

## 8.981537071084368

We try to use a linear mixed model, considering as random effects the Region variable.

md = smf.mixedlm("Score ~ PropertyRights + LaborFreedom + FiscalHealth", train, groups="Region")
mdf = md.fit()
mdf.summary()

Model:	MixedLM	Dependent Variable:	Score
No. Observations:	132	Method:	REML
No. Groups:	5	Scale:	14.1628
Min. group size:	10	Log-Likelihood:	-371.8209
Max. group size:	36	Converged:	Yes
Mean group size:	26.4

	Coef.	Std.Err.	z	P>\|z\|	[0.025	0.975]
Intercept	26.132	1.873	13.954	0.000	22.461	29.802
PropertyRights	0.391	0.023	16.752	0.000	0.345	0.437
LaborFreedom	0.120	0.027	4.364	0.000	0.066	0.174
FiscalHealth	0.106	0.012	8.773	0.000	0.083	0.130
Region Var	1.146	0.389

See http://www.statsmodels.org/stable/index.html for other commands about the linear (mixed) model. Also, https://www.statsmodels.org/stable/examples/notebooks/generated/mixed_lm_example.html makes a comparison between R lmer and Statsmodels MixedLM.

Principal Component Analysis

Import packages:

from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import numpy as np

Standardize data:

features = ['PropertyRights', 'LaborFreedom', 'GovernmentIntegrity', 'JudicalEffectiveness','FiscalHealth']
# Separating out the features
x = dt.loc[:, features].values
# Separating out the target
y = dt.loc[:,'Score'].values
# Standardizing the features
x = StandardScaler().fit_transform(x)

Perform PCA considering \(2\) principal components:

pca = PCA(4)
projected = pca.fit_transform(x)

print(x.shape)

## (173, 5)

print(projected.shape)

## (173, 4)

Plot the first \(2\) principal components:

plt.scatter(projected[:, 0], projected[:, 1],
            c=y, edgecolor='none', alpha=0.5,
            cmap=plt.cm.get_cmap('seismic', 10))
plt.xlabel('component 1')
plt.ylabel('component 2')
plt.colorbar()

## <matplotlib.colorbar.Colorbar object at 0x00000255B6038490>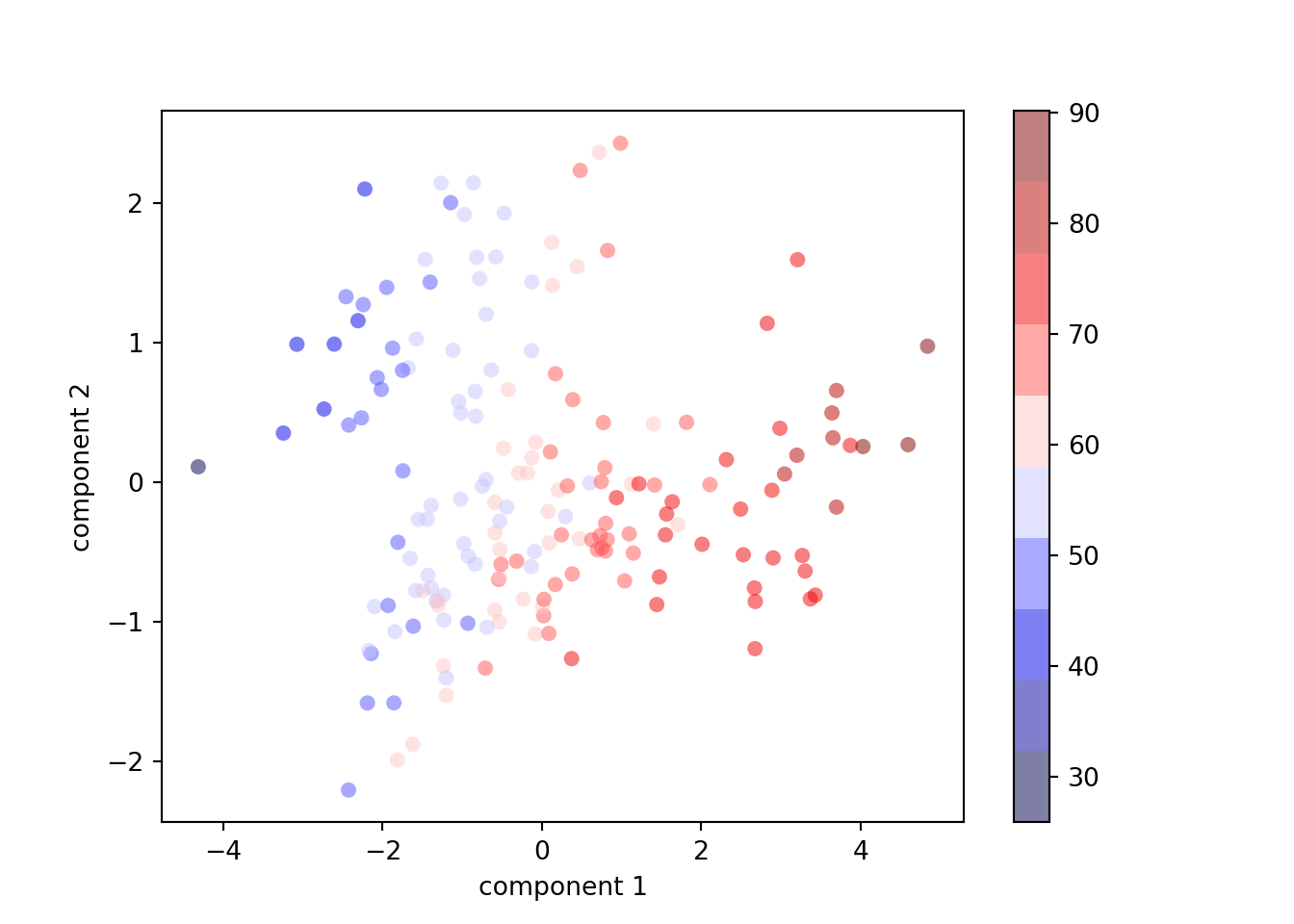

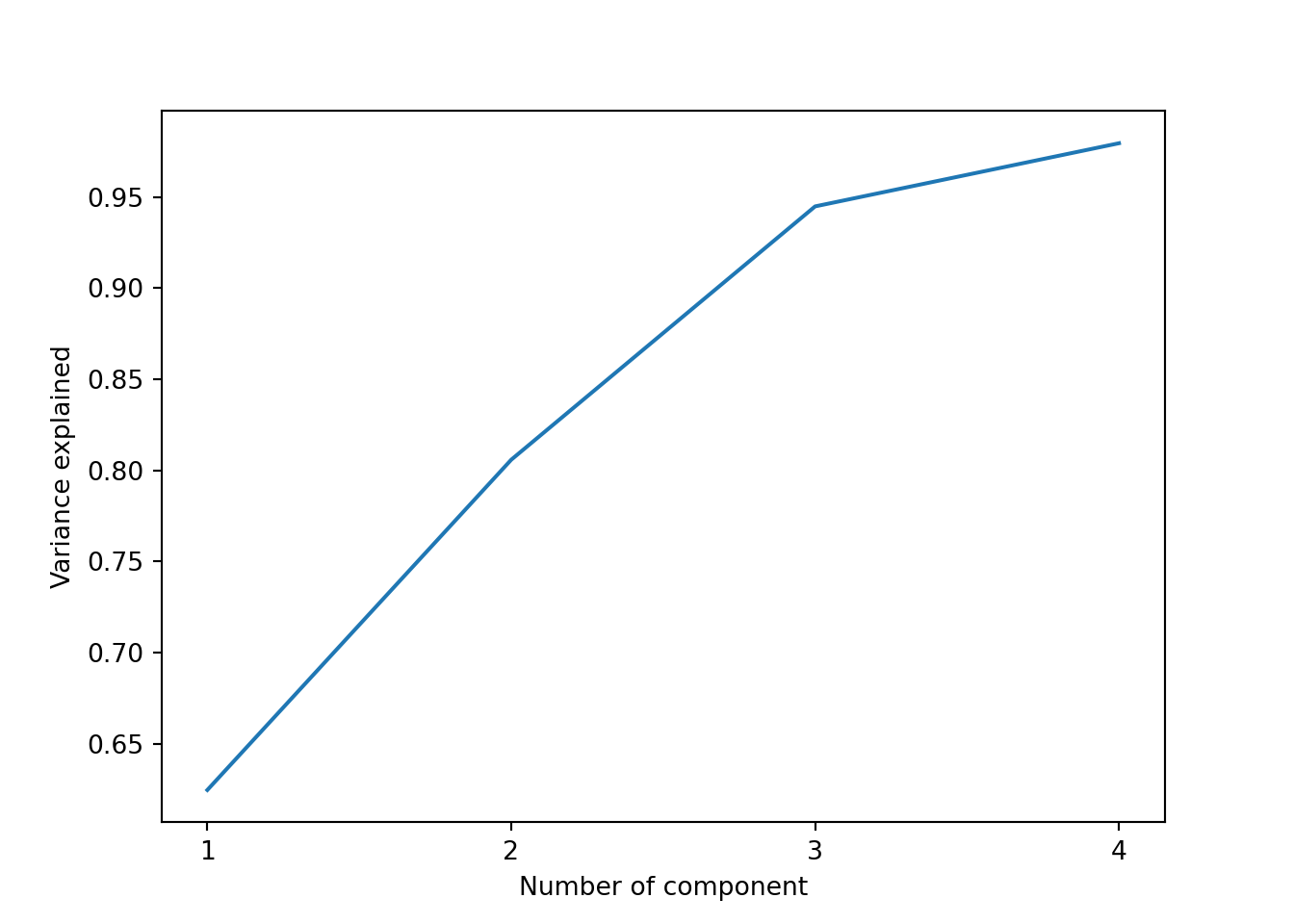
plt.plot(np.cumsum(pca.explained_variance_ratio_)) 
plt.xlabel("Number of component") 
plt.ylabel("Variance explained")
plt.xticks(range(4), [1,2,3,4])

## ([<matplotlib.axis.XTick object at 0x00000255B60C7610>, <matplotlib.axis.XTick object at 0x00000255B60C75E0>, <matplotlib.axis.XTick object at 0x00000255B60AD310>, <matplotlib.axis.XTick object at 0x00000255B61066D0>], [Text(0, 0, '1'), Text(1, 0, '2'), Text(2, 0, '3'), Text(3, 0, '4')])